Question

Below, triangle ABC has had the midpoints of sides segment AB and segment AC marked as D and E with segments DE drawn. Give a dilation, both the center and the scale factor, that would map segment DE onto segment BC. Explain why this will work.Center:Scale factor:Explanation:

Answer 1

Center of dilation: point A.

Scale factor: k=2.

Step-by-step explanation:

To find the center of dilation, we have to look at a point in that does not change its position when the dilation is applied.

This happens for point A, which when the dilation is applied to the triangle ABC won't change its position.

The scale factor can be calculated for any two pair of corresponding segments. We can pick AB and AD, that we know the relation between their lengths.

Then, the scale factor will be:

`k=\frac{\bar{AB}}{\bar{AD}}=(AD+DB)/(AD)=(2\cdot AD)/(AD)=2`

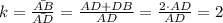
Then, the scale factor for the dilation is 2.