Question

Find the average rate of change from x = 7 to x = 14 for the function f(x) = 0.01(2)^x and select the correct answer below.

23.22
35.84
128
163.84

Answer 1

the answer is 23.22

Explanation:

Answer 2

Answer: 23.22

Explanation:

Given function:
`f(x)=0.01(2)^x`

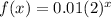
At x=7

`f(7)=0.01(2)^7=1.28`

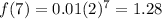
At x=14

`f(14)=0.01(2)^(14)=163.84`

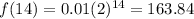
We know that the rate of change from
`x_1` to
`x_2` of function is given by

`=(f(x_2)-f(x_1))/(x_2-x_1)`

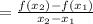
Therefore, The rate of change of given function from x=7 to x=14

`=(f(14)-f(7))/(14-7)\\\\=(163.84-1.28)/(14-7)\\\\=(162.56)/(7)\\\\=23.22`

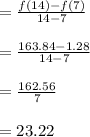
Therefore, the average rate of change from x = 7 to x = 14 for the given function is 23.22