Question

A catapult launches a boulder with an upward velocity of 112 ft/s. The height of the Boulder, h, in feet after t seconds is given by te function h=-16t^2+112t+30. How long does it take the Boulder to reach its maximum height? What is the Boulder's maximum height ? Round to the nearest hundredth , if necessary .

Please , help . I am really stuck here

Answer 1

Well we first need to do the math problem

-b/2a = -112/2(16) = 3.5 s t= 3.5s h = -16t^2 + 112t + 30 h = -16(3.5)^2 +122(3.5) +30 h = 226

adjust the windows to y=300

3.5 s; 226 ft

Answer 2

Boulder's maximum height is 226 ft.

It take 3.5 seconds the Boulder to reach its maximum height.

Explanation:

Given :

A catapult launches a boulder with an upward velocity of 112 ft/s.

The height of the Boulder, h, in feet

After t seconds is given by the function :

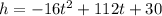`h = -16t^(2) +112t+30` --(a)

A quadratic function can be graphed using a table of values. The graph creates a parabola.

If the coefficient of the squared term is positive then the parabola opens up and The vertex of this parabola is known as the minimum point.

If the coefficient of the squared term is negative then the parabola opens down and The vertex of this parabola is known as the maximum point.

Now we will use vertex formula to calculate t

When
`f(x)= ax^(2) +bx+c`

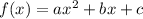
then vertex will be

`x=(-b)/(2a)`

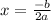
Now consider the given function:

`h = -16t^(2) +112t+30`

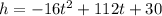
where a = -16

b=112

so using vertex formula :

`t=(-112)/(2*(-16))`

`t=3.5`

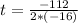
Thus, it take 3.5 seconds the Boulder to reach its maximum height.

Now to calculate the Boulder's maximum height . Put value of t = 3.5 in given function (a)

`h = -16(3.5)^(2) +112(3.5)+30`

`h = -196 +392+30`

`h = 226`

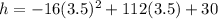
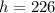
Thus, Boulder's maximum height is 226 ft.