Question

The lengths of a particular snake are approximately normally distributed with a given mean mc025-1.jpg = 15 in. and standard deviation mc025-2.jpg = 0.8 in. What percentage of the snakes are longer than 16.6 in.?

0.3%
2.5%
3.5%
5%

Answer 1

2.5% of the snakes are longer than 16.6 in

Explanation:

The Z score is,

`Z=(X-\mu)/(\sigma)`

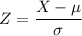
here,

X = raw score = 16.6

μ = mean = 15

σ = standard deviation = 0.8

So,

`Z=(16.6-15)/(0.8)=2`

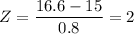
Z-score is the measurement of how many standard deviation away the data is from the mean. Hence, the value 16.6 is 2 standard deviations right to the mean.

Approximately 95% of the data falls within two standard deviations of the mean. (between the mean-2 times the standard deviation, and the mean+2 times the standard deviation)

So the 5% of data are left in the remaining space. As we have to find the amount of snakes which are longer than 16.6 in i.e we have to find the area to the right of 16.6.

The remaining 5% of amount is divided in two equal parts.

Therefore,
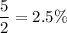`(5)/(2)=2.5\%` of the snakes are longer than 16.6 in