Question

Suiting at 6 a.m., cars, buses, and motorcycles arrive at a highway loll booth according to independent Poisson processes. Cars arrive about once every 5 minutes. Buses arrive about once every 10 minutes. Motorcycles arrive about once every 30 minutes.

(a) Find the probability that in the first 20 minutes, exactly three vehicles-two cars and one motorcycle-arrive at the booth.
(b) At the toll booth, the chance that a driver has exact change is 1/4. independent of vehicle. Find the probability that no vehicle has exact change in the first 10 minutes.
(c) Find the probability that the .seventh motorcycle arrives within 45 minutes of the third motorcycle.
(d) Find the probability that at least one other vehicle arrives at the toll booth between the third and fourth car arrival.

Answer 1

Explanation:

From the information given:

the rate of the cars =
`(1)/(5) \ car / min = 0.2 \ car /min`

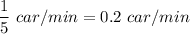
the rate of the buses =
`(1)/(10) \ bus / min = 0.1 \ bus /min`

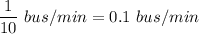
the rate of motorcycle =
`(1)/(30) \ motorcycle / min = 0.0333 \ motorcycle /min`

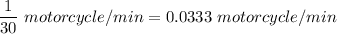
The probability of any event at a given time t can be expressed as:

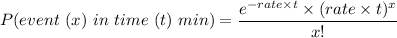
`P(event \ (x) \ in \ time \ (t)\ min) = (e^(-rate * t)* (rate * t)^x)/(x!)`

∴

(a)

`P(2 \ car \ in \ 20 \ min) = (e^(-0.20* 20)* (0.2 * 20)^2)/(2!)`

`P(2 \ car \ in \ 20 \ min) =0.1465`

`P ( 1 \ motorcycle \ in \ 20 \ min) = (e^(-0.0333* 20)* (0.0333 * 20)^1)/(1!)`

`P ( 1 \ motorcycle \ in \ 20 \ min) = 0.3422`

`P ( 0 \ buses \ in \ 20 \ min) = (e^(-0.1* 20)* (0.1 * 20)^0)/(0!)`

`P ( 0 \ buses \ in \ 20 \ min) = 0.1353`

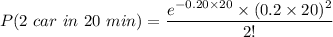
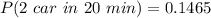
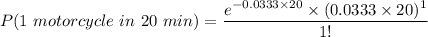
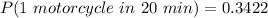
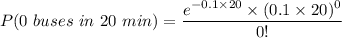
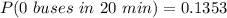
Thus;

P(exactly 2 cars, 1 motorcycle in 20 minutes) = 0.1465 × 0.3422 × 0.1353

P(exactly 2 cars, 1 motorcycle in 20 minutes) = 0.0068

(b)

the rate of the total vehicles = 0.2 + 0.1 + 0.0333 = 0.3333

the rate of vehicles with exact change = rate of total vehicles × P(exact change)

`= 0.3333 * (1)/(4)`

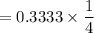
= 0.0833

∴

`P(zero \ exact \ change \ in \ 10 minutes) = (e^(-0.0833* 10)* (0.0833 * 10)^0)/(0!)`

P(zero exact change in 10 minutes) = 0.4347

c)

The probability of the 7th motorcycle after the arrival of the third motorcycle is:

`P( 4 \ motorcyles \ in \ 45 \ minutes) =(e^(-0.0333* 45)* (0.0333 * 45)^4)/(4!)`

`P( 4 \ motorcyles \ in \ 45 \ minutes) =0.0469`

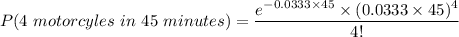
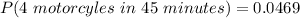
Thus; the probability of the 7th motorcycle after the arrival of the third one is = 0.0469

d)

P(at least one other vehicle arrives between 3rd and 4th car arrival)

= 1 - P(no other vehicle arrives between 3rd and 4th car arrival)

The 3rd car arrives at 15 minutes

The 4th car arrives at 20 minutes

The interval between the two = 5 minutes

For Bus:

P(no other vehicle other vehicle arrives within 5 minutes is)

=
`(6)/(12) = 0.5`

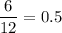
For motorcycle:

`= (2 )/(12) = (1 )/(6)`

∴

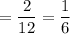
The required probability =
`1 - \Bigg ( (e^(-0.5 * 0.5^0))/(0!) * (e^(-1/6)* (1/6)^0)/(0!) \Bigg)`

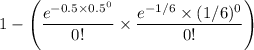
= 1- 0.5134

= 0.4866