Question

A) what is the image of (6,-12) after a dilation by a scale factor of 1/2 centered at the origin?B) The point A (-8,-5) is reflected over the point (0,-3) and it's image is point B. What are the coordinates of point B?

Answer 1

A) We calculate the scale point multypling the coordinates of the original point by the scale factor:

`\begin{gathered} P=(6,-12) \\ k=(1)/(2) \\ P\text{'}=((1)/(2)\cdot6,(1)/(2)\cdot(-12))=(3,-6) \end{gathered}`

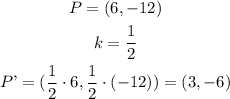
The transformed point is P'=(3,-6)

B) We have one point A=(-8,-5) that is reflected over a point C=(0,-3). The image is point B.

As it is reflected, the B point is at the same distance from C=(0,-3) than A.

We can see this in a graph:

A is at a distance of 8 units in the x-axis and 2 units in the y-axis.

Then, we add this distance to C (in the opposite direction from A) in order to get B.

B=(0,-3)+(8,2)=(8,-1).

The point B is (8,-1).