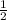Answer:
Common ratio =
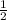
Explanation:
A sequence that progresses geometrically has the first term as 12.
Each number is the previous number divided by 2.
so the sequence will be 12, 6, 3, 1.5...........
Explicit formula of a geometric sequence is given by

Where
 = nth term of the sequence
= nth term of the sequence
a = first term
r = common ratio
and n = number of term
In this sequence common ratio =

=

=
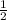
Therefore, common ratio will be