Question

The first three steps in writing f(x) = 40x + 5x2 in vertex form are shown.

Write the function in standard form. f(x) = 5x2 + 40x
Factor a out of the first two terms. f(x) = 5(x2 + 8x)
Form a perfect square trinomial. = 16
f(x) = 5(x2 + 8x + 16) – 5(16)
What is the function written in vertex form?

A.f(x) = 5(x + 4) – 80
B.f(x) = 5(x + 8) – 80
C.f(x) = 5(x + 4)2 – 80
D.f(x) = 5(x + 8)2 – 80

Answer 1

Use the formula
`(a+b)^2=a^2+2ab+b^2` for quadratic trinomial. Then you can form from a quadratic trinomial perfect square:

`x^2 + 8x + 16=x^2+2\cdot x\cdot 4+4^2=(x+4)^2`.

From the last given step you have that

`f(x) = 5(x^2 + 8x + 16)-5\cdot 16`.

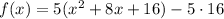Since 5·16=80, you can substitute the previous expression for perfect square into function expression and get:

`f(x)=5(x+4)^2-80`.

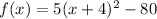This means, when x=-4, f(-4)=-80 and vertex has coordinates (-4,-80).

Answer: correct choice is C.

Answer 2

The right answer for the question that is being asked and shown above is that: "C.f(x) = 5(x + 4)2 – 80." Write the function in standard form. f(x) = 5x2 + 40x. Factor a out of the first two terms. f(x) = 5(x2 + 8x). Form a perfect square trinomial. = 16. f(x) = 5(x2 + 8x + 16) – 5(16). The vertex form is C.f(x) = 5(x + 4)2 – 80