Question

A chocolate factory produces mints that weigh 10 grams apiece. The standard deviation of the weight of a box of 10 mints is 3 grams. You buy a box of mints that weighs 95 grams. What is your confidence that the box you bought did not come from the factory?

A 90%
B 95%
C 10%
D 5%

Answer 1

The right answer for the question that is being asked and shown above is that: "C 10%." A chocolate factory produces mints that weigh 10 grams apiece. The standard deviation of the weight of a box of 10 mints is 3 grams. You buy a box of mints that weighs 95 grams.

Answer 2

Answer: Option 'A' is correct.

Explanation:

Since we have given that

Population Mean weight (
`\mu`)= 10 grams a piece

Standard deviation of the weight of a box = 3 grams

Number of mints = 10

We need to buy a box of mints that weighs 95 grams.

Sample mean is given by

`x=(95)/(10)=9.5\ grams`

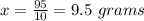
First we find out the standard error which is given by

`s=(\sigma)/(√(n))\\\\=(3)/(√(10))\\\\=0.94868`

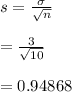
Since it is normal distribution, so, we will find z-score.

`z=(x-\mu)/(s)\\\\z=(9.5-10)/(0.94868)\\\\z=-0.527\\\\z=-0.53`

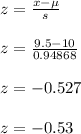
The area to the left of a z-score of -0.53 = 0.29805.

So, it may be 90% or 95 % confidence.

For 95% confidence level,

`\alpha=(1-0.95)/(2)=0.025`

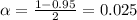
Similarly,

For 90% confidence level,

`\alpha=(1-0.90)/(2)=0.05`

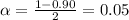
We have little confidence that the box he bought did not come from the factory. that is much smaller than 0.05.

So, it is safe to assume 90% confidence.

So, we will get 90% confidence, critical value = 1.645

Margin of error is given by

`(Standard\ deviation)* (critical\ value)\\\\=0.94868* 1.645\\\\=1.56`

So, confidence interval will be

(10-1.56,10+1.56)

=(8.44,11.56)

Hence, Option 'A' is correct.