Question

Jacob invests $8,788 in a savings account with a fixed annual interest rate compounded 6 times per year. After 4 years, the balance reaches $11,490.08. What is the interest rate of the account?

Answer 1

Given that the principal (P) is $8,788, time (T) is 4 years.

Let R be the annual rate of interest.

Given that the compounding is done 6 times a year, then the rate of interest per period and the number of periods is calculated as,

`\begin{gathered} r=(R)/(6) \\ n=6* T=6*4=24 \end{gathered}`

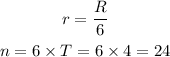
Consider the formula for amount (A) as,

`A=P(1+(r)/(100))^n`

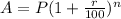
Substitute the values and simplify,

`\begin{gathered} 11490.08=8788(1+(R)/(600))^(24) \\ (1+(R)/(600))^(24)=(11490.08)/(8788) \\ 1+(R)/(600)=(1.3075)^{(1)/(24)} \\ 1+(R)/(600)=1.01123 \\ (R)/(600)=0.01123 \\ R\approx6.74 \end{gathered}`

Thus, the annual interest rate of the account is 6.74% approximately.