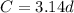When two variables x and y are proportional, the quotient between them is a constant called the constant of proportionality k:
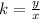
And we can write one of the variables in terms of the other by multiplying one of the variables times the constant of proportionality:
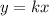
Then, to find the constant of proportionality from the table, pick a pair of data (displayed in the same row) and find the quotient between the corresponding values.
First table (s-P)
Notice that dividing a value from the column P over the corresponding value of the column s, for example, 12 and 3, we get:
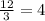
Then, the constant of proportionality is 4. Since the numerator corresponds to P and the denominator corresponds to s, we can write the equation as:
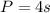
Second table (d-C)
Similarly, dividing a value from the colum C over the corresponding value of the column d, for instance, 15.7 and 5, we get:
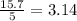
Then, the constant of proportionality is 3.14. Since the numerator corresponds to C and the denominator corresponds to d, we can write the equation as: