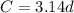Question

3) Each table represents a proportional relationship. For each, find the constant of proportionality, and write an equation that represents the relationship. d С S P 2 8 2 6.28 3 9.42 12 3 15.7 5 20 5 10 40 10 31.4 Constant of proportionality: Constant of proportionality: Equation: Equation:

Answer 1

When two variables x and y are proportional, the quotient between them is a constant called the constant of proportionality k:

`k=(y)/(x)`

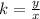
And we can write one of the variables in terms of the other by multiplying one of the variables times the constant of proportionality:

`y=kx`

Then, to find the constant of proportionality from the table, pick a pair of data (displayed in the same row) and find the quotient between the corresponding values.

First table (s-P)

Notice that dividing a value from the column P over the corresponding value of the column s, for example, 12 and 3, we get:

`(12)/(3)=4`

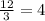
Then, the constant of proportionality is 4. Since the numerator corresponds to P and the denominator corresponds to s, we can write the equation as:

`P=4s`

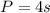
Second table (d-C)

Similarly, dividing a value from the colum C over the corresponding value of the column d, for instance, 15.7 and 5, we get:

`(15.7)/(5)=3.14`

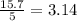
Then, the constant of proportionality is 3.14. Since the numerator corresponds to C and the denominator corresponds to d, we can write the equation as:

`C=3.14d`