Question

Which of the following statements must be true about the polynomial function f(x)?lf 1 13 is a root of f(x), then-1- 13 is also a root of f(x)13i is also a root of f(x)lf 1 13i is a root of f(x), then 1If 13 is a root of f(x), then -13 is also a root of f(x)O lf -13 t i is a root of f(x), then 13 i is also a root of f(x).

Answer 1

Answer: B is the true statement about the polynomial function.

Explanation:

If a complex number is the root of any polynomial then its conjugate is also a root of polynomial.

So only statement B is the right conditional statement telling truth about the roots of polynomial.

For example there is two polynomials
`f(x)=x-5\Rightarrow\ x=5`

is the only root of the polynomial i.e. -5 isn't the root of f(x) which contradicts the other statements.

`g(x)=x^2+4\Rightarrow\ x=-2i,+2i` Only in case of complex root the conjugate of root is also a root of the polynomial.

Answer 2

If one root of the polynomial contains square root or iota then the conjugate of that root must also be the root of that polynomial.

This is because, when we take the square root we get two answers, one positive and one negative. iota is also actually a square root i.e square root of -1.

Thus, if a polynomial has an iota or square root in one of its root, it indicates that we have taken the square root in any previous step. Since we have taken the square root, there must be two answers, which will be the conjugate of each other.

Based on this information, we can select the correct answer. The correct answer will be B. This is because 1 + 13i and 1 - 13i are the conjugates of each other.

Option A is not correct because the two roots are not conjugates of each other. The conjugate of 1 +
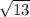
`√(13)` would have been 1 -
`√(13)`.

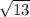
Similarly option D is also correct because the two roots are not conjugates of each other.

Thus, option B is the only correct answer