Answer:
a) For sketch see attached picture.
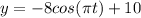
b) Mary will be able to enjoy the scenery for a total of 1.68 min or about 101 seconds.
Explanation:
a) In order to find the algebraic representation of the problem, we must start by drawing a sketch of what the problem looks like (see attached picture). Next, we can analyze it to see what function better fits the situation. In this case, since the ride starts at the lowest point, then we are talking about a negative cos function. A cos function has the followng general form:
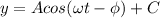
where:
A= amplitude
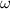 =angular speed
=angular speed
t=time
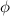 = phase shift
= phase shift
C= vertical shift.
In this case the amplitude will be the radius of the ferris wheel, so:
A=-8
it's negative because it starts at the lowest point.
the angular speed is the angle the ride will move in a given amount of time. In this case:
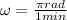
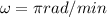
There will be no phase shift for this problem.
the vertical shift is the height of the platform, so:
C= 2
so the algebraic expression is:
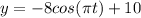
b) In order to find the total time for which she will enjoy the ride we must start by building an inequality:
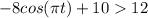
and solve it for t. We can start by turning it into an equation, solve it for t and find the answers that can be found into its domain, in this case D=[0,4]
so we get:
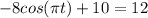
we subtract a 10 from both sides so we get:
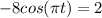
and divide 8 to both sides so we get:
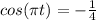
Next, we take the inverse cosine to both sides and get different answers:
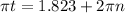
and
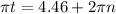
we take both equations and divide them into pi so we get:
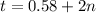
and
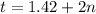
so now we find the possible answers that are between 0 and 4 minutes, this is for n=0 and 1, so we get the following times:
t={0.58, 1.42, 2.58, 3.42} min
we can now build our possible intervals for which the ferris wheel is higher than 12 m so we get the following intervals:
(0, 0.58) (0.58, 1.42) (1.42, 2.58) (2.58, 3.42) and (2.58, 4)
so we pick a test value for each of the intervals and test it on our equation. If the equation gives us a number that is greater than 12, then we have a valid interval. If we get a value that is less than 12, then we just discard that interval.
for (0, 0.58) we use 0.5 and get an answer of 10. We discard this interval.
for (0.58, 1.42) we use 1 and get an answer of 18. This is a valid interval.
for (1.42, 2.58) we use a 2 and get an answer of 2. We discard this interval.
for (2.58, 3.42) we use a 3 and get an answer of 18. This is a valid interval.
and finally, for (2.58, 4) we use a 3.5 and get an answer of 10. We discard this interval
So we have two valid intervals now: (0.58, 1.42) and (1.42, 2.58). So now we can use them to find the time for which Mary will enjoy the scenery.
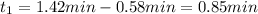
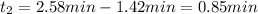
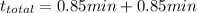
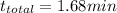
so:
Mary will be able to enjoy the scenery for a total of 1.68 min or about 101 seconds.