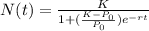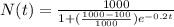Question

g There are currently 100 cases of flu in a small town of population 1,000 people, and all the people of the town are susceptible and will eventually get the flu. Early in the flu epidemic, the number of cases is increasing by 20% each day. Find a logistic function that gives the number, P, of people with the flu as a function of t, the number of days from now. SHOW WORK. Do work by hand on a piece of paper in ink and then upload a pdf of your work as your answer to this question. Your function should be in the form,

Answer 1

`N(t) = (1000)/(1 + 0.9e^(-0.2t))`

Explanation:

The logistic function has the following format:

`N(t) = (K)/(1 + ((K - P_0)/(P_0))e^(-rt))`

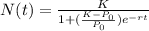
In which:

K is the carrying capacity(maximum population).

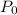`P_0` is the initial number.

r is the growth rate, as a decimal.

There are currently 100 cases of flu in a small town of population 1,000 people

This means that
`P_0 = 100, K = 1000`

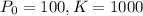
Early in the flu epidemic, the number of cases is increasing by 20% each day.

This means that
`r = 0.2`

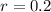
Function:

`N(t) = (K)/(1 + ((K - P_0)/(P_0))e^(-rt))`

`N(t) = (1000)/(1 + ((1000 - 100)/(1000))e^(-0.2t))`

`N(t) = (1000)/(1 + 0.9e^(-0.2t))`