Solution
- The way to solve the question is to use a formula that relates the areas and volumes of similar solids.
- The formula is given below:
![\begin{gathered} \text{ Let the dimension of the smaller solid be }l\text{ and the dimension of the bigger solid be }L \\ \text{ Let the area and volume of the smaller solid be }a\text{ and }v,\text{ and those of the bigger solide be }A\text{ and }V \\ \text{ Thus, the ratio of their areas and volumes are given as} \\ (l^2)/(L^2)=(a)/(A)\text{ \lparen Equation 1\rparen} \\ \\ (l^3)/(L^3)=((l)/(L))^3=(v)/(V)\text{ \lparen Equation 2\rparen} \\ \\ \text{ From Equation 1, we have:} \\ (l)/(L)=\sqrt{(a)/(A)} \\ \\ \text{ We can substitute this expression into Equation 2 as follows:} \\ (\sqrt{(a)/(A)})^3=(v)/(V)\text{ \lparen Equation 3\rparen} \end{gathered}]()
- Equation 3 gives us the formula that relates the areas and volumes of similar solids.
- Thus, we can apply it to solve the question as follows:
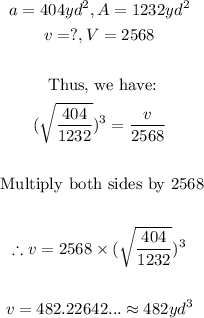
Final Answer
The volume of the smaller solid is 482yd³