Question

Use a system of equations to find the equation of the line that contains the two given points: (3, 5) and (6, 9) Write your answer in slope-intercept form.

Answer 1

First we need to create the system of equations. For a given point P, we know that:

`\begin{gathered} P(x_p,y_p) \\ \text{Then the equation of a line that passes through P is:} \\ y-y_p=m(x-x_p) \end{gathered}`

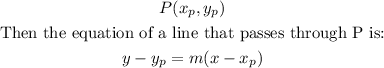
Where m is the slope. Then we can create a sistem of equations to find m:

`\begin{gathered} \text{Let }P(3,5)\text{ and }Q(6,9)\colon \\ \begin{cases}y-5=m(x-3) \\ y-9=m(x-6)\end{cases} \end{gathered}`

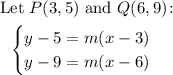
Now we let the y's alone in the left-hand side:

`\begin{cases}y=m(x-3)+5 \\ y=m(x-6)+9\end{cases}`

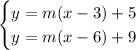
Now we can equal the two equations:

`\begin{gathered} m(x-3)+5=m(x-6)+9 \\ \end{gathered}`

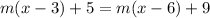
Apply distributive property and solve for m:

`\begin{gathered} mx-3m+5=mx-6m+9 \\ mx-mx-3m+6m=9-5 \\ 3m=4 \\ m=(4)/(3) \end{gathered}`

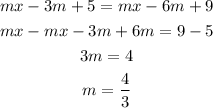
Now that we know m, we can go back to the equation of a line that passes through point P, and use P = (3, 5)

`\begin{gathered} \begin{cases}P\mleft(3,5\mright) \\ y-y_p=m(x-x_p)\end{cases} \\ y-5=(4)/(3)(x-3) \\ y=(4)/(3)x-(4)/(3)\cdot3+5 \\ y=(4)/(3)x-4+5 \\ y=(4)/(3)x+1 \end{gathered}`

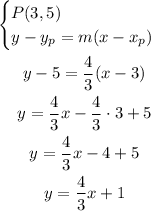
The equation of the line with the points (3, 5) and (6, 9) is y = 4/3x + 1