Question

What is fx over gx when fx is -2x^3+x^2+16x-15 and gx is x + 3

Answer 1

If f(x)=-2x³+x²+16x-15 and g(x)=x+3, we can substitute the polynomial in for f(x) and the binomial for g(x) like so:

`(2 x^(3)+ x^(2)+16x-15 )/(x+3)`

The next step is to factor the numerator by grouping in the hopes that something will cancel!

`((2 x^(3)+ x^(2)) +(16x-15) )/(x+3) \\ ( x^(2) (2x+1)+16x-15)/(x+3)`

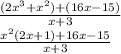
Unfortunately, because we can't factor anything out of the second grouped pair, that means there's no simplifying possible! So...

`(f(x))/(g(x)) = (2 x^(3)+ x^(2) +16x-15 )/(x+3)`

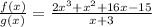
Hope this helps!