Complete Question
Consider a system consisting of an ideal gas confined within a container, one wall of which is a movable piston. Energy can be added to the gas in the form of heat by applying a flame to the outside of the container. Conversely, energy can also be removed from the gas in the form of heat by immersing the container in ice water. Energy can be added to the system in the form of work by pushing the piston in, thereby compressing the gas. Conversely, if the gas pushes the piston out, thereby pushing some atmosphere aside, the internal energy of the gas is reduced by the amount of work done.
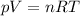
so the absolute temperature T is directly proportional to the product of the absolute pressure p and the volume V,Here n denotes the amount of gas moles,which is a constant because the gas is confined and R is the universal constant
What is the
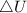 as the system of ideal gas goes from point A to point B on the graph recall u is proportional to T
as the system of ideal gas goes from point A to point B on the graph recall u is proportional to T
Answer:

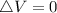
The gas A and B have same internal energy
Step-by-step explanation:
From the question we are told that
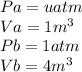
Generally the equation of temperature is mathematically given as


And
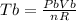
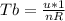
Generally the change in temperature
 is mathematically given as
is mathematically given as
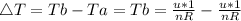

Generally the change in internal energy
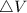

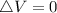
Therefore with

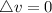
The gas A and B have same internal energy