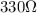Question

Compute the resistance in ohms of a lead block 15 cm long and 0.10 cm2 in cross-sectional area. (ρ = 2.2 x 10-5 ohm-cm)

Answer 1

Answer: The resistance of a lead block is
`330\Omega`

Step-by-step explanation:

Resistance is defined as the difficulty of flowing of electric current through a substance. It is directly proportional to the length of the wire and inversely proportional to the area of cross section of the wire.

Mathematically,

`R\propto (l)/(A)`

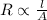
Removing the proportionality sign, we get:

`R=\rho (l)/(A)`

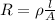
Where,

`\rho` = Resistivity of the wire =
`2.2* 10^(-5)\Omega cm`

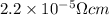
R = Resistance of the wire = ? ohm

l = Length of the wire = 15 cm

A = Area of cross-section of the wire =
`15cm^2`

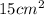
Putting the values in above equation, we get:

`R=(2.2* 10^(-5)\Omega cm* 15cm)/(0.10cm^2)`

`R=330\Omega`

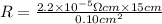
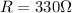
Hence, the resistance of a lead block is
`330\Omega`

Answer 2

Resistance of a wire is defined as the measure of how difficult an electric current will pass through a conductor. The longer the wire, the greater the resistance. Resistivity, on the other hand, is an intrinsic property depending on the material to which the current passes. The formula for resistance in terms of resistivity is:

R = pL/A

where:
R = resistance
p = resistivity
L = length
A = cross-sectional area

This gives a resistance of 3.3x10^-3 ohms