Explanation:
For a. We must find the lim as x approaches 2 from the right.
We can use direct substitution for the second equation because
- We can direct subsitute since we not dealing with no asymptotes
- We use the second equation because that is when x is greater than or equal to two so we use that because we can determine the limit.
So just subsitue 2 in for x.
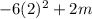
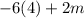

So the limit as x approaches 2 from the right, is 2m-24.
b. We now must find the limit as x approaches 2 from the left,
This time we will use the top equation because since the x values for the top equation is only defined to be less than 2, we can know the behavior as it approaches 2 from the left.
Here we direct subsitue again
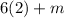
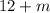
So as x approaches 2 from the left, the limit is 12+m
Here we let
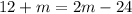
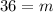
The value is 36 so
m=36