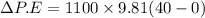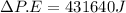Answer:
Change in kinetic energy=-513.652 KJ
Change in potential energy=431.64KJ
Step-by-step explanation:
We are given that
Mass of an automobile , m=1100 kg
Initial speed, u=110 km/h=

Where
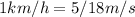
Height ,
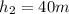
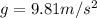
Final speed, v=0
Change in kinetic energy,


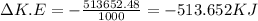
Where 1 KJ=1000 J
Change in potential energy,
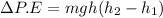
Initially height, h1=0
Using the formula