Question

A random sample of Democrats and a random sample of Republicans were polled on an issue. Of 100 Republicans, 69 would vote yes on the issue; of 200 democrats, 123 would vote yes. Let pl and p2 denote respectively the proportions of all Democrats or all Republicans who would vote yes on this issue. Use the R script to finish the following questions.

(a) Construct a 95% confidence interval for pl - p2
(b) Can we say that more Democrats than Republicans favor the issue at the 1% level of significance.

Answer 1

Explanation:

(a)

For the two proporion confidence interval p1-p2

# by default R = 95% confidence interval

The R-code = prop.test(X = c(123,690, n=c (200, 100))

where;

x - takes favorable cases

n - sample size

(b)

Here;

`H_o : p_1 =p_2`

`H_1 : p_1 > p_2`

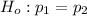
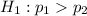
The R-code = prop.test (X = c(123,690, n=c (200, 100)), alternative = "greater", conf.int = 0.99)

Now;

From the information given;

out of 200 democrats, 123 voted yes;

`p_1 = (123)/(200)`

`p_1 = 0.615`

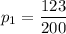
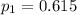
Since 69 voted yes out of 100 republicans, then:

`p_2 = (69)/(100)`

`p_2 =0.69`

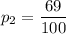
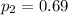
For pooled proportion;

`\hat p = (n_1p_1+n_2p_2)/(200 + 100)`

`\hat p = (123+69)/(200 + 100)`

`\hat p = (192)/(300)`

`\hat p = 0. 64`

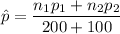
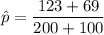
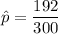
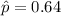
Since p = 0.64

Then; q = 1 - p

q = 1 - 0.64

q = 0.36

∴

The confidence interval for the difference in population proportion

`= (p_1 - p_2 ) \pm z_(\alpha/2) \sqrt{(pq)((1)/(n_1)+(1)/(n_2)) }`

`C.I = 1 - \alpha \\ \\ C.I = 1 - 0.95 = 0.05`

`z_(\alpha /2) = z_(0.05 /2) \\ \\ z_(0.025) = 1.96`

∴

`= (0.615- 0.69) \pm 1.96 \sqrt{(0.64 * 0.36)((1)/(100)+(1)/(200)) }`

`= -0.075 \pm 0.11522`

`= (-0.075 - 0.11522,-0.075 + 0.11522)`

`= (-0.19022,0.04022)`

∴

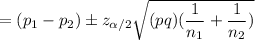
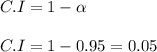
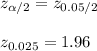
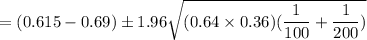
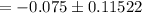
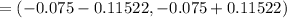
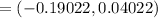
Lower limit = -0.19022

upper limit = 0.04022

Thus; the 95% confidence interval lies between:

-0.19022 < p1 - p2 < 0.04022

b)

Recall that:

Null hypothesis:

`H_o :p_1 = p_2`

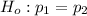
Alternative hypothesis:

`H_1 : p_1 > p_2`

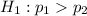
This is a right-tailed test.

The z test statistics can be computed as:

`z = \frac{\hat p_1 - \hat p_2}{\sqrt{pq((1)/(n_1) + (1)/(n_2) )}}`

`z = \frac{0.615 -0.69}{\sqrt {(0.64*0.36) ((1)/(100) + (1)/(200) )}}`

`z = -1.276`

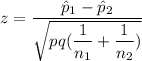
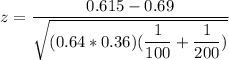
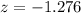
P-value = P(Z > -1.276)

P-value = 0.899

Decision rule: Reject the null hypothesis if P-value < level of significance at 0.01

Conclusion: We fail to reject the null hypothesis since P-value is greater than the level of significance and we conclude that there is insufficient evidence to say that more democrats favor the issue at the 1% level of significance than the republicans.