Question

Find 3x2 - y3 - y3 - z if x = 3, y = -2, and z = -5.

Answer 1

Hello,


`3 x^(2) -y^(3) -y^(3)-z \\ =3 x^(2) -2y^(3)-z \\ \\ Replacing:\,\, \,\,x=3\,\, \,\,y=-2\,\, \,\,z=-5 \\ \\ =3(3)^(2) -2(-2)^(3)-(-5) \\ =3*9-2*(-8)+5 \\ =27+16+5 \\ =48`

Answer: 48

Answer 2

The value of
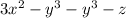`3x^2-y^3-y^3-z` is, 48

Explanation:

Given the equation:

Let f(x, y, z) =
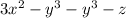`3x^2-y^3-y^3-z` .....[1]

Like terms states that the terms which have the same variables.

Combine like terms in equation [1];

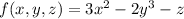`f(x, y, z) =3x^2-2y^3-z` ......[2]

Given: x= 3 , y= -2 and z = -5.

Substitute these given values in [2] we get;

`f(3, -2, -5) =3(3)^2-2(-2)^3-(-5)`

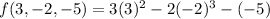
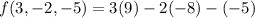`f(3, -2, -5) =3(9)-2(-8)-(-5)` = 27 + 16 +5 = 48.

Therefore, the value of
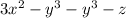`3x^2-y^3-y^3-z` is, 48