We can directly remove m^12 from the square root, and stay only with 98 inside the square root
![\sqrt[]{98m^(12)}=m^{(12)/(2)}\sqrt[]{98}=m^6\sqrt[]{98}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/r2vwcegaqy5c2yoyp6yx.png)
Therefore
![\sqrt[]{98m^(12)}=m^6\sqrt[]{98}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/p137qf41eyw8db8isifi.png)
Now we can just factor 98 inside the square root:
Then
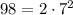
We can put it inside the square root
![\begin{gathered} m^6\, \sqrt[]{98}=m^6\, \sqrt[]{2\cdot7^2} \\ \\ \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ps1eo4p3p8jl8kcowwc2.png)
Now we can simplify the square with the square root
![m^6\, \sqrt[]{2\cdot7^2}=7m^6\, \sqrt[]{2}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/34ipqk77evvi5eyqkagl.png)
That's the final result
![\sqrt[]{98m^(12)}=7m^6\, \sqrt[]{2}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ph8cdh5qgc46ty9wzw2z.png)