Question

Find the remainder when f(x)=x^88+5x-2 is divided by (x + 1)

Answer 1

d. -6

Step-by-step explanation:

By the remainder theorem, we get that:

`f(x)=(x+1)\cdot q(x)+r`

Where q(x) is another polynomial and r is the remainder.

To eliminate the value of q(x), we will replace x by -1 to get:

`\begin{gathered} f(-1)=(-1+1)\cdot q(-1)+r \\ f(-1)=0\cdot q(x)+r \\ f(-1)=r \end{gathered}`

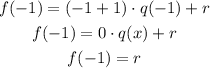
But f(x) = x^(88) + 5x - 2, so f(-1) will be equal to:

`\begin{gathered} f(x)=x^(88)+5x-2 \\ f(-1)=(-1)^(88)+5(-1)-2 \\ f(-1)=1-5-2 \\ f(-1)=-6_{} \end{gathered}`

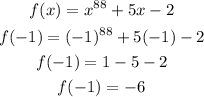
Therefore, if f(-1) = -6 and f(-1) = r, we get that

r = -6

So, the remainder is d. -6