When a ball is launched with some angle from a point then the components of velocity of ball can be expressed as,
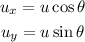
The displacement of the ball along x-axis and y-axis can be given as,
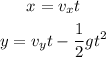
Plug in the known values,
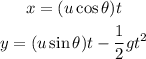
The final velocity of the ball along y-axis is,
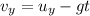
At the maximum height the final velocity is zero. Substitute the known values,
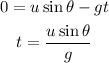
This time is for motion of ball upto maximum height therefore, the total time is given as,
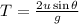
The horizontal range of the ball can be given as,
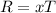
Substitute the known values,
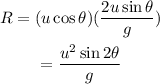
When the ball is launched diagonally then the angle is 45 degree which makes the range of ball as,
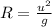
because, sin90=1.
Plug in the known values,
![\begin{gathered} 1.02\text{ m=}(u^2)/(9.8m/s^2) \\ u^2=(1.02m)(9.8m/s^2) \\ u=\sqrt[]{9.996m^2s^(-2)} \\ \approx3.16\text{ m/s} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/tik6ntp75psrljhj138g.png)
Therefore, the initial velocity of the ball is 3.16 m/s.
The time taken by ball to reach the highest point is,
![t=\sqrt[]{(2h)/(g)}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/fd5nx86oxwlgsbfc1h9e.png)
Plug in the known values,
![\begin{gathered} t=\sqrt[]{\frac{2(1\text{ m)}}{9.8m/s^2}} \\ \approx0.452\text{ s} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/1ht2arywk3eqegb7307u.png)
Thus, the time taken by ball to reach at highest point is 0.452 s.
The final velocity of ball is given as,
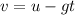
Plug in the known values,
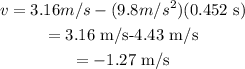
Thus, the final speed of the ball is -1.27 m/s in which negative sign indicates that the ball is deaccelerating.