Question

Hello this is a projectile motion question. I need help with a

Answer 1

When a ball is launched with some angle from a point then the components of velocity of ball can be expressed as,

`\begin{gathered} u_x=u\cos \theta \\ u_y=u\sin \theta \end{gathered}`

The displacement of the ball along x-axis and y-axis can be given as,

`\begin{gathered} x=v_xt \\ y=v_yt-(1)/(2)gt^2 \end{gathered}`

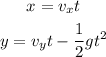
Plug in the known values,

`\begin{gathered} x=(u\cos \theta)t \\ y=(u\sin \theta)t-(1)/(2)gt^2 \end{gathered}`

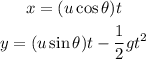
The final velocity of the ball along y-axis is,

`v_y=u_y-gt`

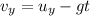
At the maximum height the final velocity is zero. Substitute the known values,

`\begin{gathered} 0=u\sin \theta-gt \\ t=(u\sin \theta)/(g) \end{gathered}`

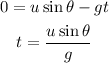
This time is for motion of ball upto maximum height therefore, the total time is given as,

`T=(2u\sin \theta)/(g)`

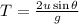
The horizontal range of the ball can be given as,

`R=xT`

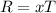
Substitute the known values,

`\begin{gathered} R=(u\cos \theta)((2u\sin \theta)/(g)) \\ =(u^2\sin 2\theta)/(g) \end{gathered}`

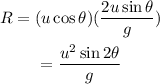
When the ball is launched diagonally then the angle is 45 degree which makes the range of ball as,

`R=(u^2)/(g)`

because, sin90=1.

Plug in the known values,

`\begin{gathered} 1.02\text{ m=}(u^2)/(9.8m/s^2) \\ u^2=(1.02m)(9.8m/s^2) \\ u=\sqrt[]{9.996m^2s^(-2)} \\ \approx3.16\text{ m/s} \end{gathered}`

Therefore, the initial velocity of the ball is 3.16 m/s.

The time taken by ball to reach the highest point is,

`t=\sqrt[]{(2h)/(g)}`

Plug in the known values,

`\begin{gathered} t=\sqrt[]{\frac{2(1\text{ m)}}{9.8m/s^2}} \\ \approx0.452\text{ s} \end{gathered}`

Thus, the time taken by ball to reach at highest point is 0.452 s.

The final velocity of ball is given as,

`v=u-gt`

Plug in the known values,

`\begin{gathered} v=3.16m/s-(9.8m/s^2)(0.452\text{ s)} \\ =3.16\text{ m/s-}4.43\text{ m/s} \\ =-1.27\text{ m/s} \end{gathered}`

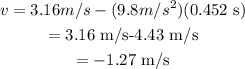
Thus, the final speed of the ball is -1.27 m/s in which negative sign indicates that the ball is deaccelerating.