Question

Seventy-nine percent of products come off the line ready to ship to distributors. Your quality control department selects 12 products randomly from the line each hour. Looking at the binomial distribution, if fewer than how many are within specifications would require that the production line be shut down (unusual) and repaired?

a. Fewer than 7
b. Fewer than 9
c. Fewer than 6
d. Fewer than 10

Answer 1

c. Fewer than 6

Explanation:

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

Can be approximated to a normal distribution, using the expected value and the standard deviation.

The expected value of the binomial distribution is:

`E(X) = np`

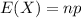
The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

In the binomial distribution, an outcome is considered unusual if it is more than 2.5 standard deviations below the mean.

Seventy-nine percent of products come off the line ready to ship to distributors.

This means that
`p = 0.79`

Your quality control department selects 12 products randomly from the line each hour.

This means that
`n = 12`

Mean:

`E(X) = np = 12*0.79 = 9.48`

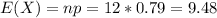
Standard deviation:

`√(V(X)) = √(np(1-p)) = √(12*0.79*0.21) = 1.41`

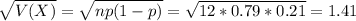
Unusual:

`9.48 - 2.5*1.41 = 5.96`

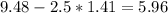
So fewer than 6 is considered unusual.