Answer:
a.
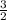
b.
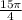
c.
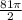
d.
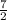
Explanation:
P.S - The exact question is -
a.
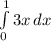
y = 3x
Shape of the given integral = A Triangle
Area of Triangle =
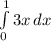 =
=
 ×1×3 =
×1×3 =
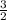
The graph of integral is as follows :
b.
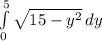
x =
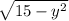
⇒x² = 15 - y²
⇒x² + y² = 15
⇒x² + y² = (√15)²
Shape of the integral = Quarter circle of radius √15
Area of Quarter circle =
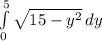 =
=
 ×
×
 ×r² =
×r² =
 ×
×
 ×(√15)² =
×(√15)² =
The graph of the following integral is as follows :
c.
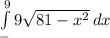
y =
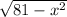
⇒y² = 81 - x²
⇒y² + x² = 81
⇒y² + x² = 9²
Shape of the integral = Semi circle of radius 9
Area of semi circle =
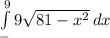 =
=
 ×
×
 ×r² =
×r² =
 ×
×
 ×9² =
×9² =
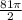
The graph of the following integral is as follows :
d.

x = 5 -
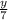
⇒
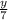 = 5 - x
= 5 - x
⇒y = 35 - 7x
At y = 0 , x = 5
At y = 7 , x = 4
Shape of the integral = A triangle
Area of Triangle =
 ×(5-4)×7 =
×(5-4)×7 =
 ×(1)×7 =
×(1)×7 =
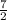
The graph of the integral is as follows :