Question

Consider the function f(x)=x^2-5. If g(x)=f(x-7), what can be said about g(x)? Check all that apply

Answer 1

f(x) = x^2 - 5
g(x) = f(x - 7)

g(x) = f(x - 7)
g(x) = (x - 7)^2 - 5
g(x) = (x - 7)(x - 7) - 5
g(x) = (x(x - 7) - 7(x - 7)) - 5
g(x) = (x(x) - x(7) - 7(x) + 7(7)) - 5
g(x) = (x^2 - 7x - 7x + 49) - 5
g(x) = (x^2 - 14x + 49) - 5
g(x) = x^2 - 14x + 49 - 5
g(x) = x^2 - 14x + 44

Answer 2

For this case we have the following function:

`image`

We apply the following function transformation:

Horizontal translations

Suppose that h> 0

To graph y = f (x-h), move the graph of h units to the right.

For h = 7 we have:

`image`

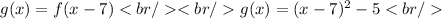
Answer:

The following statements are correct:

1)
`image`

2) The graph of g (x) is the graph of f (x) with a displacement of 7 units to the right