Answer:
D. 0.200, 0.026
Explanation:
For each teen, there are only two possible outcomes. Either they have a fax machine, or they do not. The probability of a teen having a fax machine is independent of other teens. So we use the binomial probability distribution to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
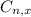 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.
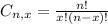
And p is the probability of X happening.
Forty-three percent of US teens have heard of a fax machine.
This means that
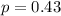
You randomly select 12 US teens.
This means that

Find the probability that the number of these selected teens that have heard of a fax machine is exactly six (first answer listed below).
This is
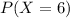 . So
. So

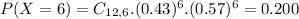
So the answer is either option B or D.
Find the probability that the number is more than 8
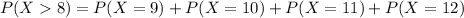

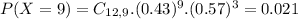
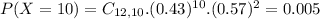
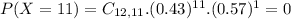
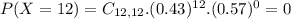
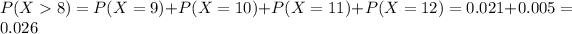
So the correct answer is given by option D.