Question

Question 2. Determine the relative maxima and minima of f(x)=2x³-3x². Also describewhere the function is increasing and decreasing:

Answer 1

The given function is:

`f(x)=2x^3-3x^2`

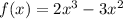
It is required to find the relative maxima and minima, and then describe where the function is increasing or decreasing.

Find the derivative of the function:

`\begin{gathered} f^(\prime)(x)=3(2)x^(3-1)-2(3)x^(2-1) \\ \Rightarrow f^(\prime)(x)=6x^2-6x \end{gathered}`

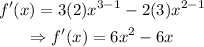
Substitute f'(x)=0 to find the critical points:

`\begin{gathered} 6x^2-6x=0 \\ Factor\text{ the expression on the left:} \\ \Rightarrow6x(x-1)=0 \\ \text{ Equate the factors to zero:} \\ \Rightarrow6x=0\text{ or }x-1=0 \\ \Rightarrow x=0\text{ or }x=1 \end{gathered}`

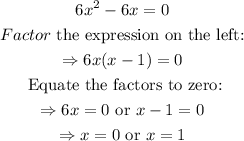
Find the second derivative of the function:

`\begin{gathered} f^(\prime)(x)=6x^2-6x \\ \text{ Find the derivative of both sides:} \\ \Rightarrow f^(\doubleprime)\left(x\right)=12x-6 \end{gathered}`

Substitute the critical points x=0 and x=1 into the second derivative:

`\begin{gathered} f^(\doubleprime)\left(0\right)=12(0)-6=-6 \\ f^(\doubleprime)\left(1\right)=12(1)-6=6 \end{gathered}`

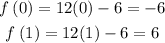
Since the second derivative is negative at x=0, it follows from the second derivative test, that the function is maximum at x=0.

Since the second derivative is positive at x=1, it follows from the second derivative test, that the function is minimum at x=1.

Next, calculate the function values at x=0, and x=1:

`\begin{gathered} f(x)=2x^3-3x^2 \\ \Rightarrow f(0)=2(0)^3-3(0)^2=0 \\ \Rightarrow f(1)=2(1)^3-3(1)^2=2-3=-1 \end{gathered}`

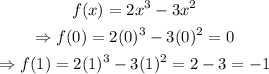
The relative maximum is 0 at x=0.

The relative minimum is -1 at x=-1.

Recall that a function is increasing in the interval where its derivative is positive (greater than 0), while it is decreasing in the interval where its derivative is negative (less than 0).

To find the interval where the function is increasing, solve the inequality f'(x)>0:

`\begin{gathered} 6x^2-6x>0 \\ \Rightarrow6x(x-1)>0 \\ \text{ list the possible solutions:} \\ x<0,\;01 \\ Picking\text{ arbitrary numbers in the interval and checking if the inequality holds:} \\ \text{ The solution is:} \\ x<0\text{ or }x>1 \\ \Rightarrow(-$ \infty $,0)\cup(1,$ \infty $) \end{gathered}`

To find the interval where the function is decreasing, solve the inequality f'(x)<0:

[tex]\begin{gathered} 6x^2-6x<0 \\ \text{ Using the same procedure as the first inequality, the solution is:} \\ 0The function is increasing in the interval (-∞,0) U (1,∞).

The function is decreasing in the interval (0,1).