Question

The SAT mathematics scores in the state of Florida for this year are approximately normally distributed with a mean of 500 and a standard deviation of 100.

Using the empirical rule, what is the probability that a randomly selected score lies between 500 and 700? Express your answer as a decimal.

Answer 1

0.4772

Explanation:

Mean =
`\mu = 500`

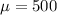
Standard deviation =
`\sigma = 100`

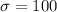
Now we are supposed to find the probability that a randomly selected score lies between 500 and 700.

Formula :
`z=(x-\mu)/(\sigma)`

At x = 500

`z=(500-500)/(100)`

`z=(0)/(100)`

At x = 700

`z=(700-500)/(100)`

`z=(200)/(100)`

`z=2`

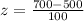
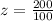
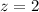
Now to find P(500<z<700)

P(0<z<2) =P(z<2)-P(z<0)

Now using z table :

P(z<2)-P(z<0) =0.9772-0.5000=0.4772

Thus the probability that a randomly selected score lies between 500 and 700 is 0.4772.

Answer 2

The answer to the problem presented above is .475. Using the empirical rule, the probability that a randomly selected score lies between 500 and 700 (which is 2 standard deviations above the mean) is .475 or 47.5%.