Question

The number of column inches of classified advertisements appearing on Mondays in a certain daily newspaper is normally distributed with population mean of 320 and population standard deviation of 20 inches. For a randomly chosen Monday, what is the probability there will be between 280 and 360 column inches of classified advertisement?

Answer 1

The probability there will be between 280 and 360 column inches of classified advertisement

P(280≤X≤360) = P(-2≤Z≤2) = 0.9544

Explanation:

Step(i):-

Given that the mean the population = 320

The standard deviation of the Population = 20

Let 'X' be the random variable in a normal distribution

Let 'X' = 280

`Z = (x-mean)/(S.D) = (280-320)/(20) = -2`

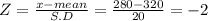
Let 'X' = 360

`Z = (x-mean)/(S.D) = (360-320)/(20) = 2`

Step(iii):-

The probability there will be between 280 and 360 column inches of classified advertisement

P(280≤X≤360) = P(-2≤Z≤2)

= P(z≤2) -P(z≤-2)

= P(z≤2)+P(z≤2)

= 2P(z≤2)

= 2×0.4772 ( from normal table)

= 0.9544