Question

A golf ball strikes a hard, smooth floor at an angle of 28.2 ° and, as the drawing shows, rebounds at the same angle. The mass of the ball is 0.0260 kg, and its speed is 42.8 m/s just before and after striking the floor. What is the magnitude of the impulse applied to the golf ball by the floor? (Hint: Note that only the vertical component of the ball's momentum changes during impact with the floor, and ignore the weight of the ball.)

Answer 1

I = 1.06886 N s

Step-by-step explanation:

The expression for momentum is

I = F t = Δp

therefore the momentum is a vector quantity, for which we define a reference system parallel to the floor

Let's find the components of the initial velocity

sin 28.2 = v_y / v

cos 28.2= vₓ / v

v_y = v sin 282

vₓ = v cos 28.2

v_y = 42.8 sin 28.2 = 20.225 m / s

vₓ = 42.8 cos 28.2 = 37.72 m / s

since the ball is heading to the ground, the vertical velocity is negative and the horizontal velocity is positive, it can also be calculated by making

θ = -28.2

v_y = -20.55 m / s

v_x = 37.72 m / s

X axis

Iₓ = Δpₓ =
`p_(fx) - p_(ox)`

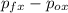
since the ball moves in the x-axis without changing the velocity, the change in moment must be zero

Δpₓ = m
`v_(fx)` - m v₀ₓ = 0

v_{fx} = v₀ₓ

therefore

Iₓ = 0

Y axis

I_y = Δp_y = p_{fy} -p_{oy}

when the ball reaches the floor its vertical speed is downwards and when it leaves the floor its speed has the same modulus but the direction is upwards

v_{fy} = - v_{oy}

Δp_y = 2 m v_{oy}

Δp_y = 2 0.0260 (20.55)

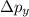`\Delta p_(y)` = 1.0686 N s

the total impulse is

I = Iₓ i ^ + I_y j ^

I = 1.06886 j^ N s