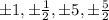Question

Use the rational zero theorem to list all possible rational zero's for the polynomial function: f(x)=2x^3+3x^2-8x+5 To earn full credit please share all work, calculations and thinking. If you prefer you can do the work by hand on a piece of paper, take a picture of that work and upload it.

Answer 1

The given polynomial function is:

`f(x)=2x^3+3x^2-8x+5`

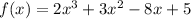
Since all the co-efficients are integers, we can apply the rational zero theorem.

The trailing co-efficient ( the co-efficient of the constant term) is 5.

Find its factors with the plus and minus sign; thus we have;

`\begin{gathered} \text{Factors}=\pm1,\pm5 \\ \text{These are the possible values for p} \end{gathered}`

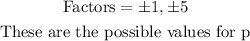
The leading co-efficient ( the co-efficient of the term with the highest degree) is 2.

Find its factors with the plus and minus sign; thus we have:

`\begin{gathered} \text{Factors}=\pm1,\pm2 \\ \text{These are the }possible\text{ values for q} \end{gathered}`

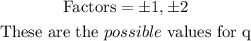
Next, is finding all possible values for the rational expression p/q. Thus, we have:

`\begin{gathered} (p)/(q)=\pm(1)/(1),\pm(1)/(2),\pm(5)/(1),\pm(5)/(2) \\ (p)/(q)=\pm1,\pm(1)/(2),\pm5,\pm(5)/(2) \end{gathered}`

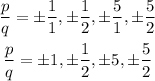
Hence, the possible rational zeros for the polynomial function are:

`\pm1,\pm(1)/(2),\pm5,\pm(5)/(2)`