Answer:
The value of the test statistic is of 0.22.
Explanation:
Our test statistic is:
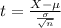
In which X is the sample mean,
 is the expected mean,
is the expected mean,
 is the standard deviation(square root of the variance) and n is the size of the sample.
is the standard deviation(square root of the variance) and n is the size of the sample.
A lumber company is making boards that are 2920.0 millimeters tall.
This means that
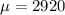 .
.
A sample of 12 is made, and it is found that they have a mean of 2922.7 millimeters with a variance of 121.00.
This means that
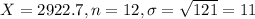 . So
. So
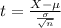
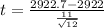
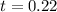
The value of the test statistic is of 0.22.