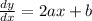Question

A student club is designing a trebuchet for launching a pumpkin into projectile motion. Based on an analysis of their design, they predict that the trajectory of the launched pumpkin will be parabolic and described by the equation y(x) =ax^2+bx where a=−8.0×10^−3m^−1, b=1.0(unitless), x is the horizontal position along the pumpkin trajectory and y is the vertical position along the trajectory. The students decide to continue their analysis to predict at what position the pumpkin will reach its maximum height and the value of the maximum height.

Required:
What is the derivative of the vertical position of the pumpkin trajectory with respect to its horizontal position?

Answer 1

`(dy)/(dx)=2ax+b`

Step-by-step explanation:

We are given that

`y(x)=ax^2+bx`

`a=-8.0* 10^(-3)m^(-1)`

`b=1.0`

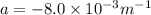
x=Horizontal position along the trajectory

y=Vertical position along the trajectory

We have to find the derivative of the vertical position of the pumpkin trajectory with respect to its horizontal position.

Differentiate the equation w.r.t x

`(dy)/(dx)=2ax+b`

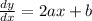
Hence, the derivative of the vertical position of the pumpkin trajectory with respect to its horizontal position is given by

`(dy)/(dx)=2ax+b`