Explanation:
- -4x - y = 19 -------- Equation ( i )
- x - 2y = -7 ----------- Equation ( ii )
From equation ( i ) :
-4x - y = 19
-y = 19 + 4x
-y = - ( -19 - 4x )
y = -4x - 19 ------ Equation ( iii )
Substituting the value of y from equation ( iii ) in equation ( ii ) , we get :
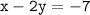
⇾
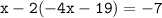
⇾
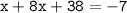
⇾
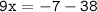
⇾
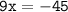
⇾
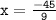
⇾

Substituting the value of x in equation ( i ) , we get :
⇾
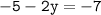
⇾
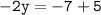
⇾
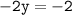
⇾
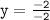
⇾
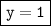
The possible solution of the system is ordered pair ( x , y ) = ( -5 , 1 ) .

Hope I helped ! ツ
Have a wonderful day / night ! ♡
▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁