Question

John is playing a game of darts. The probability that he throws a dart into the center of the dart board (the Bull’s eye) is 1/10. The probability that he throws the dart into the 10-point ring is 3/10.

What is the probability that he either hits a Bull’s eye or scores 10 points?
a. 1/3
b. 2/3
c. 3/5
d. 2/5
e. 1/4

Answer 1

Answer: The correct option is (d).
`(2)/(5).`

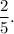
Step-by-step explanation: Given that John is playing a game of darts. The probability that he throws a dart into the centre of the dart board (the Bull’s eye) is
`(1)/(10)` and the probability that he throws the dart into the 10-point ring is
`(3)/(10).`

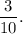
We are to find the probability that he either hits a Bull’s eye or scores 10 points.

Let, 'A' and 'B' represents the events that John throws the dart into a Bull's eye and 10-point ring respectively.

Then, according to the given information, we have

`P(A)=(1)/(10),~~P(B)=(3)/(10),~~~P(A\cup B)=?`

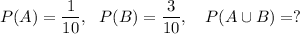
Since John cannot throw the dart into the Bull's eye and 10 point ring together, both the events are independent of each other.

Therefore,

`P(A\cap B)=0`

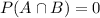
From the theorems of probability, we have

`P(A\cup B)=P(A)+P(B)-P(A\cap B)=(1)/(10)+(3)/(10)-0=(4)/(10)=(2)/(5).`

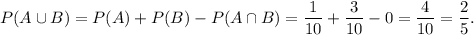
Therefore, the probability that John either hits a Bull’s eye or scores 10 points is
`(2)/(5).`

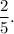
Thus, (d) is the correct option.

Answer 2

The correct answer for the question that is being presented above is this one: "d. 2/5." John is playing a game of darts. The probability that he throws a dart into the center of the dart board (the Bull’s eye) is 1/10. The probability that he throws the dart into the 10-point ring is 3/10. The probability that he either hits a Bull's eye or scores 10 points is 2/5