Question

Suppose that the event of picking a face card from a standard deck of 52 cards is considered a success. If a card is drawn at random and replaced, and this process is repeated 11 times, what is the probability that the card selected was a face card 6 times?

a. 0.019
b. 0.024
c. 0.004
d. 0.976
e. 0.995

Answer 1

i think it might be d or e    0.995 or 0.976

Answer 2

0.019

Explanation:

Number of face cars = 12

Total number of cards =52

So, Probability of getting face card =
`(12)/(52)`

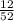
Probability of not getting face card =
`1-(12)/(52)=(40)/(52)`

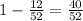
Now we are given that a card is drawn at random and replaced, and this process is repeated 11 times so, what is the probability that the card selected was a face card 6 times

So, we will use binomial

Success is getting a face card

Failure is not getting a face card

Formula :
`P(X=r)=^nC_r p^r q^(n-r)`

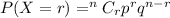
p = probability of success =
`(12)/(52)`

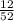
q = Probability of failure =
`(40)/(52)`

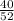
n = no. of trials = 11

r = no. of times getting success = 6

Substitute then values in the formula

`P(X=6)=^(11)C_6 ((12)/(52))^6 ((40)/(52))^(11-6)`

`P(X=6)=^(11)C_6 ((12)/(52))^6 ((40)/(52))^(5)`

`P(X=6)=0.019`

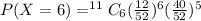
Hence If a card is drawn at random and replaced, and this process is repeated 11 times, the probability that the card selected was a face card 6 times is 0.019.