Question

A circle is centered at the point (-3, 2) and passes through the point (1, 5). The radius of the circle is ______ units. The point (-7, ______) lies on this circle.

How would I do this?

Answer 1

circle formula
(x-h)^2+(y-k)^2=r^2 where (h,k) is the center
and r=radius

to find the radius
we are given one of the points and the center
distnace from them is the radius
distance formula
D=
`\sqrt{(x2-x1)^(2)+(y2-y1)^(2)}`
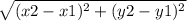
points (-3,2) and (1,5)
D=
`\sqrt{(1-(-3))^(2)+(5-2)^(2)}`
D=
`\sqrt{(4)^(2)+(3)^(2)}`
D=
`√(16+9)`
D=
`√(25)`
D=5

center is -3,2
r=5
input
(x-(-3))^2+(y-2)^2=5^2
(x+3)^2+(y-2)^2=25 is equation
radius =5
input -7 for x and solve for y
(-7+3)^2+(y-2)^2=25
(-4)^2+(y-2)^2=25
16+(y-2)^2=25
minus 16
(y-2)^2=9
sqqrt
y-2=+/-3
add 2
y=2+/-3
y=5 or -1

the point (-7,5) and (7,-1) lie on this circle



radius=5 units
the points (-7,5) and (-7,1) lie on this circle