Answer:
The semi truck travels at an initial speed of 69.545 meters per second downwards.
Step-by-step explanation:
In this exercise we see a case of an entirely inellastic collision between the semi truck and the car, which can be described by the following equation derived from Principle of Linear Momentum Conservation: (We assume that velocity oriented northwards is positive)
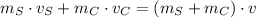 (1)
(1)
Where:
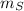 ,
,
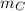 - Masses of the semi truck and the car, measured in kilograms.
- Masses of the semi truck and the car, measured in kilograms.
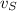 ,
,
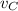 - Initial velocities of the semi truck and the car, measured in meters per second.
- Initial velocities of the semi truck and the car, measured in meters per second.
 - Final speed of the system after collision, measured in meters per second.
- Final speed of the system after collision, measured in meters per second.
If we know that
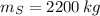 ,
,
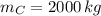 ,
,
 and
and
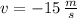 , then the initial velocity of the semi truck is:
, then the initial velocity of the semi truck is:
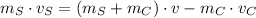
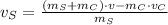
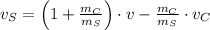
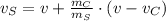
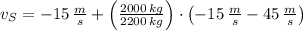

The semi truck travels at an initial speed of 69.545 meters per second downwards.