Question

Juanagui asked May 24, 2023

83,973 views

1 Answer

Temor · Answer 1 · 2023-05-29T20:52:34+0000

EXPLANATION

Let's see the facts:

$\text{Ratio}=\frac{1+\sqrt[]{5}}{2}$

Dimenstions of the garden:

$\text{Width = 26 f}eet$
$\text{Path = x}$

The length of the garden is given by the following relationship:

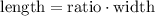
$\text{length}=\text{ratio}\cdot\text{width}$

Replacing terms:

$\text{length}=\frac{1+\sqrt[]{5}}{2}\cdot26=13(1+\sqrt[]{5})$

Applying the distributive property:

$\text{length =13 + 13 }\sqrt[]{5}$

Simplifying:

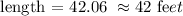
$\text{length = 42.06 }\approx42\text{ fe}et$

2) If the gardener wants to plant a tomato for every 3 square feet, we need to divide the area of the garden by the required area.

Area of the garden = Length * Width = 26ft * 42 ft = 1092 ft^2

Dividing by the area of each tomato give us the appropiate relationship:

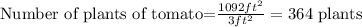
$\text{Number of plants of tomato=}(1092ft^2)/(3ft^2)=364\text{ plants}$

There would be needed 364 plants of tomato.

3) The area of the path that surrounds the garden could be obtained by the following relationship:

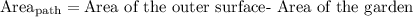
$\text{Area}_{\text{path}}=\text{Area of the outer surface- Area of the garden}$

The area of the outer surface can be obtained by the following relationship:

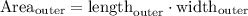
$\text{Area}_{\text{outer}}=\text{length}_{\text{outer}}\cdot\text{width}_{\text{outer}}$

Replacing terms:

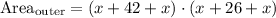
$\text{Area}_{\text{outer}}=(x+42+x)\cdot(x+26+x)$

Adding like terms:

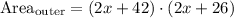
$\text{Area}_{\text{outer}}=(2x+42)\cdot(2x+26)$

Applying the distributive property:

$\text{Area}_{\text{outer}}=4x^2+52x+84x+68$

Adding like terms:

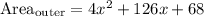
$\text{Area}_{\text{outer}}=4x^2+126x+68$

Then, subtracting the outer and the garden area give us the area of the path:

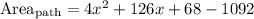
$\text{Area}_{\text{path}}=4x^2+126x+68-1092$

Subtracting numbers:

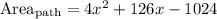
$\text{Area}_{\text{path}}=4x^2+126x-1024$

The expression that represents the area of the path is 4x^2+126x -1024

Your comment on this question: