Question

Using the ideal gas equation, calculate the pressure of oxygen gas in a cylinder with a volume of 25.00 L. The oxygen masses 4.362 kg and room temperature is at 22.5 o C. How many moles of oxygen are there and what is the pressure of oxygen in atmospheres in the cylinder according to the ideal gas law?

Answer 1

Equation: PV=nRT
Rearrange: P=nRT/V
Mols of oxygen = m/M = 4362g/16g/mol
=272.625
P=272.625*8.314*(22.5+273.15)/25
=26804 pascales
=0.26453491Atmosphere

Answer 2

Answer : The number of moles present in the oxygen gas is, 272.625 moles and the pressure of oxygen gas in atmosphere in the cylinder is, 264.56 atm

Solution : Given,

Mass of oxygen gas = 4.362 Kg = 4362 g (1 Kg = 1000 g)

Molar mass of oxygen gas = 16 g/mole

First we have to calculate the moles of oxygen gas.

`\text{Moles of oxygen gas}=\frac{\text{Mass of oxygen gas}}{\text{Molar mass of oxygen gas}}=(4362g)/(16g/mole)=272.625moles`

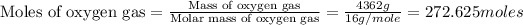
Now we have to calculate the pressure of oxygen gas by using ideal gas equation.

`PV=nRT\\\\P=(nRT)/(V)`

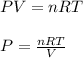
where,

P = pressure of gas

T = temperature of gas =
`22.5^oC=273+22.5=295.5K`

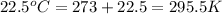
V = volume of gas = 25 L

n = number of moles of gas = 272.625 moles

R = gas constant = 0.0821 Latm/moleK

Now put all the given values in the ideal gas equation, we get the pressure of gas.

`P=((272.625moles)* (0.0821Latm/moleK)* (295.5K))/(25L)=264.56atm`

Therefore, the number of moles present in the oxygen gas is, 272.625 moles and the pressure of oxygen gas in atmosphere in the cylinder is, 264.56 atm