Answer:
D) Replace the 7/8 with a 5/6.
Explanation:
Given,
The original value of the scooter = $ 8000,
If it loses an eighth of its value.
Then the decrement in the price of scooter =
 of the original price of the scooter
of the original price of the scooter


Now, the final price of the scooter = Original price of the scooter - Decrement in price




Similarly, If it loses an sixth of its value.
Then, decrement in price =
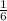 of 8000
of 8000

And, the final price of the scooter =




Hence, Option D is correct.