Question

Complete the algebra tile grid to model the product of (x+2) (x-3) remove the zero pairs. Then rewrite the product in simplest form.

Answer 1

`1 x^(2) + -1 x + -6`

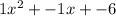
Explanation:

Fill in the left side of the grid with the first factor, x + 2 , and fill in the top of the grid with the second factor, x - 3 . Then complete the inside of the grid using the outside tiles as the length and the width of the inside area.

Next cancel out any zero pairs. In this model, two pairs of x and -x tiles can be canceled out.

So the expression (x + 2)( x - 3) is rewritten as
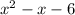`x^(2) - x - 6`.

Answer 2

The given expression is,

`(x+2)(x-3)`

Apply FOIL Method:

`\mleft(a+b\mright)\mleft(c+d\mright)=ac+ad+bc+bd`

Therefore,

`\begin{gathered} \mleft(x+2\mright)\mleft(x-3\mright)=xx+x\mleft(-3\mright)+2x+2\mleft(-3\mright) \\ =xx+x\mleft(-3\mright)+2x+2\mleft(-3\mright) \end{gathered}`

Simplify

`x^2-3x+2x-6=x^2-x-6`

Hence, the product in its simplest form is

`x^2-x-6`