Question

Factor perfect square trinomials 75u^3 - 30u^2v + 3uv^2

Answer 1

3u(5u-v)²

STEP - BY - STEP EXPLANATION

What to do?

Factor the given trinomials.

Given:

`75u^3-30u^2v+3uv^2`

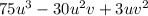
To solve, we will follow the steps below:

Step 1

Factor out 3u from the given trinomials, since 3u is common to all the terms.

`3u(25u^2-10uv+v^2)`

Step 2

Further factorize 25u² - 10uv + v²

Step 3

Find two terms such that its product gives 25u²v² and its sum gives -10uv.

The two terms are -5uv and -5uv.

Step 4

Replace the -10uv by the two terms.

That is;

`3u(25u^2-5uv-5uv+v^2)`

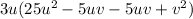
Step 4

Factorize the inner parenthesis.

`3u\lbrack5u(5u-v)-v(5u-v)\rbrack`
`3u(5u-v)(5u-v)`
`=3u(5u-v)^2`

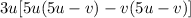
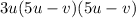
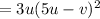
Therefore, the factorized form is 3u(5u-v)²