Question

Two containers designed to hold water are side by side, both in the shape of acylinder. Container A has a diameter of 18 feet and a height of 9 feet. Container B hasa diameter of 16 feet and a height of 11 feet. Container A is full of water and the wateris pumped into Container B until Conainter B is completely full.To the nearest tenth, what is the percent of Container A that is empty after thepumping is complete?

Answer 1

To answer this question we will use the following formula to compute the volume of a cylinder:

`\text{Volume}=(diameter^2)/(4)\cdot\pi\cdot\text{height.}`

Therefore, the volume of container A is:

`V_A=((18ft)^2)/(4)\cdot\pi\cdot9ft=729\pi ft^3\text{.}`

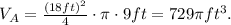
The volume of container B is:

`V_B=((16ft)^2)/(4)\cdot\pi\cdot11ft=704\pi ft^3\text{.}`

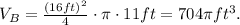
Now, after pumping the water, the percent of container A that is empty is:

`(V_B)/(V_A)*100=(704\pi ft^3)/(729\pi ft^3)*100.`

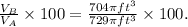
Simplifying the above result we get:

`(70400)/(729)\approx96.6.`

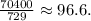
Answer: 96.6%